Table of Contents
Introduction to relative atomic mass
An atom is too small and measurement of its mass by an instrument is not a practical solution for day-to-day science. As a result, we need to understand the mass of an atom with respect to a standard. The masses of proton, neutron and electron have been determined experimentally. Through various experiment, the isotope of carbon - C-12 has been found to be the most suitable standard to express the masses of all other elements (including all the isotopes).
Out of this need, the concept of Relative Atomic Mass has been born. It is defined as:
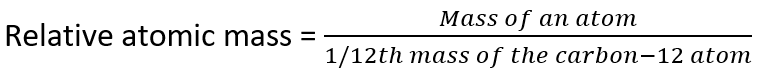
In other words, it is a mass of an atom, relative to the mass of C-12. Since it is a ratio, it is unitless.
For example, let’s consider Magnesium-24. Its RAM will be:
![]()
We can clearly see that is is numerically equal to the atomic mass. So, the obvious question is why do we need it at all?
The answer lies in the natural abundance of isotopes. The isotopes of an element have different masses, due to the presence of the different number of neutrons. Whenever we take a sample of an element, the ratio of the natural abundance is reflected in the sample. As we know, one mole of any element will have 6.02214179 x 1023 number of atoms. This is a huge number and there will be billions of atoms for each of the isotopes, according to the natural abundance. Since the practicality of measuring the mass of each and every atom is out of the question, we have to resort to the RAM. This is also known as the atomic weight. It is the weighted average of all the atoms as per the natural abundance.
Let’s take the example of Chlorine. It has two stable isotopes namely 35Cl and 37Cl. In the periodic table, however, the mass of a chlorine atom is given as 35.45 u. This results from the relative abundance of 75.76% of chlorine-35 and 24.24% of chlorine-37.
A similar method is followed in case of molecules and the mass of a molecule relative to that of C-12 is called the Relative Molecular Mass (RMM).
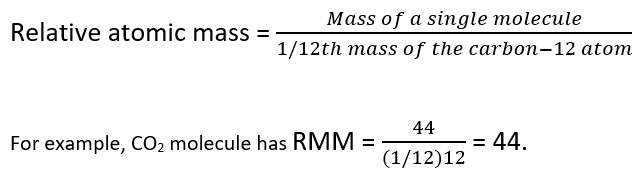
Relevance of RAM and RMN in Mass spectrometry
Mass Spectrometry is founded on the principle of separation of the charged particles in vacuum through the force exerted by the magnetic and electric fields. This separation is a result of the mass-to-charge ratio (m/z OR m/e) of individual ionic fragments. Often, the ions produced during mass spectrometry are singly charged (z=1), which effectively shortens the mass-to-charge ratio to the more easily calculated term mass.
The technique of mass spectrometry can distinguish any number of isotopes an element may have. The output is presented in a xy plot where the x-axis represents the mass-to-charge ratio and the y-axis represents the relative abundance. When applied to a sample of a pure element, the mass spectrometry reveals each isotope as a separate peak. This technique can be used not only for identifying the relative abundance of isotopes in a sample of an element, but also to identify the presence and percentage of each element in a compound. Since the relative abundance of isotopes is used in this technique, the y-axis does not have any unit and hence, the highest among the peaks obtained in a mass spectrum is assigned as the “base peak” and taken as 100% (not to be confused with the total abundance of each element). All the other peaks are assigned as a percentage of the base peak.
Read more about high-resolution mass spectroscopy
Identifying the RAM and RMN from mass spectra and its usefulness in structural analysis.
Let’s take an example of the mass spectrum of a sample of Boron. It shows two peaks having relative isotopic masses of 10 and 11 on the C-12 scale. The y-axis is designated as “Relative abundance” where the isotope with mass is assigned as the “base peak” with a relative abundance of 100.
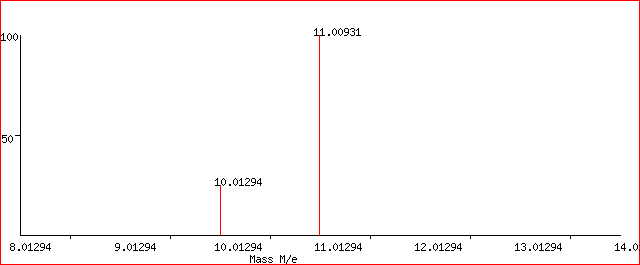
In this case, the relative abundances of the two isotopes are:
boron-10 23
boron-11 100
In this case, we would consider the total number of atoms to be 100 + 23 = 123.
Hence, the total mass of the isotopes = (23 x 10) + (100 x 11) = 1330.
The average mass would therefore be, the total mass divided by the total number of atoms.
i.e. 1330/123 = 10.8 which is the relative atomic mass (RAM) of Boron.
The other method is to express the y-axis as the “Relative abundance %”. The mass spectrum of Zirconium is shown below.
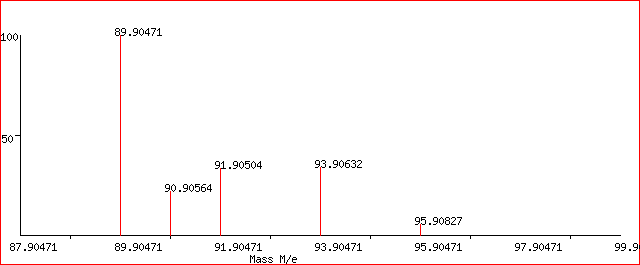
The relative abundances are given as percentages. The 5 peaks are of relative isotopic masses of 90, 91, 92, 94 and 96 on the C-12 scale.
In this case, the relative abundance % of the 5 isotopes are:
zirconium-90 51.5
zirconium-91 11.2
zirconium-92 17.1
zirconium-94 17.4
zirconium-96 2.8
In this case, we would consider the total number of atoms to be 100.
The total mass would then be (51.5 x 90) + (11.2 x 91) + (17.1 x 92) + (17.4 x 94) + (2.8 x 96) = 9131.8
Hence, the RAM = 9131.8 / 100 = 91.3 for Zr.
A similar calculation can be done for compounds. Since these comprise of molecules, the term we should find is the Relative Molecular Mass (RMM).
An example of chlorobenzene molecule can help in understanding the utility of mass spectrometry in differentiating the subtleties in the above-mentioned terms and its effectiveness in dealing with isotopes.
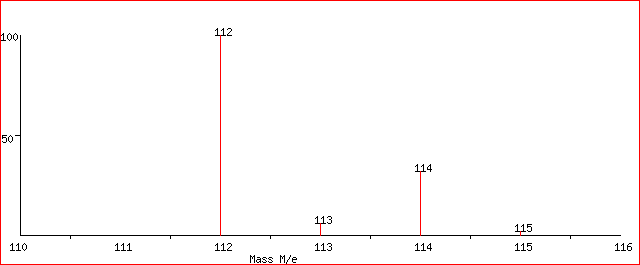
This is the mass spectrum of chlorobenzene with the natural abundance of all isotopes.
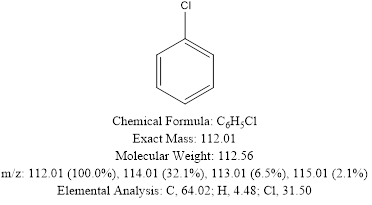
It can be clearly seen that the chlorobenzene with a natural abundance of both isotopes of chlorine has a MW of 112.56 which is also called the RMM.
Key Points:
1. RAM is a mass of an atom, relative to the mass of C-12. Since it is a ratio, it is unitless.
2. RMM is a mass of a molecule, relative to the mass of C-12. Since it is a ratio, it is unitless.
3. The mass spectrum is obtained as a xy plot where the x-axis represents the mass-to-charge ratio and the y-axis represents the relative abundance or relative abundance %.
4. The highest peak is taken as the “base peak” and in the relative abundance method, it is assigned as 100% and all other peaks are assigned as a percentage of that.
5. A mass spectrum can identify the number and percentage of isotopes present in a compound.
Frequently Asked Questions
What is relative atomic mass?
Relative atomic mass is the ratio of the mass of an element to 1/12th of the mass of a carbon atom. Relative atomic mass depends on the relative abundance of different isotopes of an element.
What is mass spectrometry?
Mass spectrometry is a technique which is used to separate different isotopes of an element and to calculate their relative abundances. It works on the principle; that when charged particles move through electric and magnetic fields in a vacuum, they get separated on the basis of their mass-to-charge ratio.
What is relative abundance?
Different isotopes of an element are present in different proportions in a naturally occurring sample of an element. Relative abundance means the percentage of a certain isotope of an element in a naturally occurring sample.
Is relative atomic mass same as mass number?
No. mass number is the sum of protons and neutrons present in the nucleus of an atom and it is a whole number value while relative atomic mass is the ratio of the mass of an element to the 1/12th of the mass of a carbon atom. RAM can be in decimal form.
Frequently Asked Questions
What is relative atomic mass?
Relative atomic mass is the ratio of the mass of an element to 1/12th of the mass of a carbon atom. Relative atomic mass depends on the relative abundance of different isotopes of an element.
What is mass spectrometry?
Mass spectrometry is a technique which is used to separate different isotopes of an element and to calculate their relative abundances. It works on the principle; that when charged particles move through electric and magnetic fields in a vacuum, they get separated on the basis of their mass-to-charge ratio.
What is relative abundance?
Different isotopes of an element are present in different proportions in a naturally occurring sample of an element. Relative abundance means the percentage of a certain isotope of an element in a naturally occurring sample.
Is relative atomic mass the same as the mass number?
No, the mass number is the sum of protons and neutrons present in the nucleus of an atom and it is a whole number value while relative atomic mass is the ratio of the mass of an element to the 1/12th of the mass of a carbon atom. RAM can be in decimal form.
References:
1. https://www.youtube.com/watch?v=-xqTwkaiDps
2. http://www.sisweb.com/mstools/isotope.htm
3. http://www.chemguide.co.uk/analysis/masspec/elements.html





