Table of Contents
Key Facts & Summary of Enthalpy Changes
- The enthalpy of a chemical system refers to the "heat content" of the system.
- Enthalpy is given the symbol H
- Enthalpy change refers to the amount of heat released or absorbed when a chemical reaction and it is given the symbol ΔH
- A reaction is exothermic when it releases energy, and ΔH = negative.
- A reaction is defined endothermic when it absorbs energy, therefore the ΔH = positive.
Enthalpy
The amount of heat evolved or absorbed in a reaction carried out at constant pressure is called enthalpy changes. It is given the symbol ΔH, read as "delta H".
It is important to remember that The term "enthalpy change" only applies to reactions done at constant pressure. The standard enthalpy changes apply when the reaction is run at standard conditions, which are :
- 298 K (25°C)
- a pressure of 1 bar (100 kPa).
- where solutions are involved, a concentration of 1 mol dm-3
Also, the compounds need to be present in their standard state. That is the physical and chemical state that you would expect to find it in under standard conditions.
That means that the standard state for water, for example, is liquid water, - not steam or water vapour or ice.
Oxygen's standard state is the gas, - not liquid oxygen or oxygen atoms.
Enthalpy changes are calculated using Hess's law:
If a process can be written as the sum of several steps, the enthalpy change of the process equals the sum of the enthalpy changes of the individual steps.
If we know the enthalpy changes of a series of reactions that add up to give an overall reaction, we add these enthalpy changes to determine the enthalpy change of the overall reaction.
If we know the standard enthalpies of formation, ΔH, of the reactants and products of a reaction we can calculate the enthalpy change of the reaction using the following shorthand version of Hess's law:
![]()
Where Σ ΔH indicate the sum of the change of enthalpies.
Hess's Law is says that if you convert reactants A into products B, the overall enthalpy change will be exactly the same whether you do it in one step or two steps or however many steps.
A reaction is exothermic when it releases energy, and ΔH = negative. On the other hand, a reaction is defined endothermic when it absorb energy, therefore the ΔH = positive.
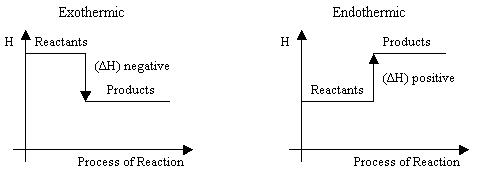
Scheme 1. Graphic representation of changes of enthalpy in the reactions.
In an exothermic reaction
- Heat is a product of the reaction.
- Temperature of reaction mixture increases.
- Hproducts < Hreactants
- ΔH = Hproducts - Hreactants = a negative number
In an endothermic reaction
- Heat is a reactant in the reaction.
- Temperature of reaction mixture decreases.
- Hproducts > Hreactants
- ΔH = Hproducts - Hreactants = a positive number
Let's have a look now to the following picture:
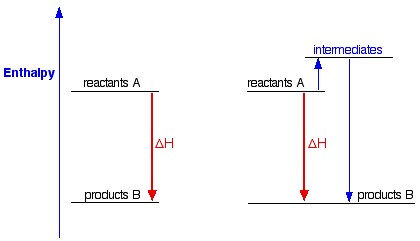
This shows a chemical reaction between the same reagents, producing the same products, but going through two different ways. In one case, there is a direct conversion; in the other, there is a two-step process involving some intermediates.
As you can see, in either case, the overall enthalpy change is the same, because it is governed by the relative positions of the reactants and products on the enthalpy diagram.
If you go via the intermediates, you do have to put in some extra heat energy to start with, but you get it back again in the second stage of the reaction sequence.
This is true for any reaction.
Let's use an example and explore better this topic:
H2O2(l) → H2O(l) + 1/2 O2(g); ΔH = -98.2 kJ
The symbol for a standard enthalpy change of reaction is ΔH°r. For enthalpy changes of reaction, the "r" (for reaction) is often missed off - it is just assumed.
The "kJ mol-1" (kilojoules per mole) refers to the quantities of all the substances given in the equation. In this case, 98.2 kJ of heat is evolved when 1 moles of hydrogen peroxide liquid reacts to form 1 mole of water liquid and 1 moles of oxygen gas.
Whenever a standard enthalpy change is quoted, standard conditions are assumed. If the reaction has to be done under different conditions, a different enthalpy change would be recorded. But this is a problem for another time.
Let's use the same reaction in a usual enthalpy problem:
Hydrogen peroxide decomposes according to the following thermochemical reaction:
H2O2(l) → H2O(l) + 1/2 O2(g); ΔH = -98.2 kJ
How do we calculate the change in enthalpy, ΔH, when 1.00 g of hydrogen peroxide decomposes in this reaction?
First of all, we need to know the enthalpy change value, which is given here. If it is not given, there are tables indicating them.
The thermochemical equation tells us that ΔH for the decomposition of 1 mole of H2O2 is -98.2 kJ.
Now, we need to know the number of moles of the relevant compound to calculate the answer. We use the Periodic Table to add up the masses of hydrogen and oxygen atoms in hydrogen peroxide: the molecular mass of H2O2 is 34.0 (2 x 1 for hydrogen + 2 x 16 for oxygen), which means that 1 mol H2O2(l) = 34.0 g H2O2
Using these data we can calculate:
ΔH = 1.00 g H2O2 x 1 mol H2O2 / 34.0 g H2O2 x -98.2 kJ / 1 mol H2O2
ΔH = -2.89 kJ
Let's use another example and take in consideration the following reaction:
CS2(l) + 3 O2(g) → CO2(g) + 2 SO2(g)
Given values:
C(s) + O2(g) → CO2(g); ΔH = -393.5 kJ/mol
S(s) + O2(g) → SO2(g); ΔH = -296.8 kJ/mol
C(s) + 2 S(s) → CS2(l); ΔH = 87.9 kJ/mol
To solve this type of problem, we can follow a few rules:
-The reaction can be reversed. This will change the sign of ΔH.
-The reaction can be multiplied by a constant.
-The value of ΔH must be multiplied by the same constant. Any combination of the first two rules may be used.
Let's start finding one of the reactants or products where there is only one mole in the reaction. In our case, one CO2 and the first reaction has one CO2 on the product side.
C(s) + O2(g) →CO2(g), ΔH= -393.5 kJ/mol
This gives us the CO2 we need on the product side and one of the O2 moles we need on the reactant side. To get two more O2 moles, use the second equation and multiply it by two. Remember to multiply the ΔH by two as well.
2 S(s) + 2 O2(g) → 2 SO2(g), ΔH = 2(-326.8 kJ/mol)
Now we have two extra S and one extra C molecule on the reactant side.
The third reaction also has two S and one C on the reactant side. Reverse this reaction to bring the molecules to the product side. Remember to change the sign on ΔHf.
CS2(l) → C(s) + 2 S(s), ΔHf = -87.9 kJ/mol
When all three reactions are added, the extra two sulfur and one extra carbon atoms are canceled out, leaving the target reaction. All that remains is adding up the values of ΔH
ΔH = -393.5 kJ/mol + 2(-296.8 kJ/mol) + (-87.9 kJ/mol)
ΔH = -393.5 kJ/mol - 593.6 kJ/mol - 87.9 kJ/mol
ΔH = -1075.0 kJ/mol
Therefore, the answer to our initial question, the change in enthalpy for the above reaction is -1075.0 kJ/mol.
Read more about Enthalpy and Entropy
Frequently Asked Questions
What is enthalpy change?
The amount of heat energy absorbed or released during a chemical process is called enthalpy change. It is represented by ΔH.
What is Hess's law?
Hess's law states that if a chemical process occurs in many steps, the overall enthalpy change of the process is the sum of enthalpy changes of the individual steps.
What are the different types of enthalpy changes?
Enthalpy changes may take place in the form of the heat of neutralization, heat of combustion, heat of solution, heat of formation, lattice energy, etc.
What is the unit of enthalpy?
The S.I unit of enthalpy is Joule (J).
Further readings
https://www.chemguide.co.uk/physical/energetics/definitions.html
Clayden Jonathan Clayden, Nick Geeves, Stuart Warren ISBN: 978-0199270293





