Bond Enthalpy

Summary

Bond enthalpy, also referred to as bond energy or bond dissociation energy, is the energy required to break a particular covalent bond in one mole of molecule in a gaseous state. The term was previously used as “bond strength.” These terms have the same exact meaning; therefore, they can be used interchangeably. 

Bond Enthalpy for Diatomic Molecules

For diatomic molecules (molecules consisting of 2 same (H₂) or different (HBr) atoms), bond energy (D_X-Y) can also be defined as the standard enthalpy change for an endothermic reaction.

D – represents the bond energy in kilojoules per mole (kJ/mol), which is always a positive number. 

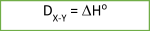
For the following general reaction:

XY(g) → X(g) + Y(g)

Let’s consider a specific example:

• There is a pure covalent bond in the H₂ molecule between the 2 H atoms (H-H)
• D_H-H = ∆H^o = 436 kJ/mol (given value)
• So, the bond energy to break a pure covalent bond between H atoms is equal to 436kJ per mole of H-H bonds broken.
• H₂(g) → 2H(g)
• So, hydrogen atoms take 436kJ to break up 1 mole of gaseous hydrogen molecules
• Therefore, bond energy for the H-H bond is 436 kJ/mol or 436 kJ∙mol^-1

Bond Enthalpy for Molecules with 3 or More Atoms

When we have a more complicated molecule composed of 3 or more atoms, we should consider all the bonds in the molecule. So, the standard enthalpy change for the endothermic reaction through which all the bonds in the molecule are broken would be the sum of all bond energy values. 

Let’s consider the following molecule:

• CH₄ – methane
• Consists of 4 covalent C-H bonds
• CH₄ (g) → C(g) + 4H(g)
• D_C-H = 415 kJ/mol (given value)
• Therefore, ∆H^o = 4 ∙ D_C-H = 4 ∙ 415 kJ/mol = 1660 kJ/mol

Even though there are 4 identical C-H bonds in the CH₄ molecule, the energy required to break each bond is not the same. Once the first C-H bond is broken, the next bond requires less energy to break. The given value of 415 kJ/mol is just an average value. For that reason, many bond enthalpy values are provided as average (or mean) bond enthalpies, also referred to as bond enthalpy terms.

Moreover, bond enthalpies for different complex molecules are given as average values. For instance, the C-H bond might be surrounded by different molecules, which means that the bond enthalpy should probably be different. Although, the bond enthalpy value for C-H is the same, which means that the calculations using the given values are not that reliable.  

Considering the bond energies per mole, we can determine which bond is stronger. Generally, bond strength increases with increasing the number of electron pairs in the bond. For that reason, double bonds are stronger than single bonds; Therefore, they require more energy input to break down. Similarly, triple bonds are stronger than both single and double bonds. 

We can also predict which bond is stronger when one atom bonds to different atoms in a group. The bond strength generally decreases as we move down the group. For example, bond energy for C-F is 439 kJ/mol, for C-Cl – 330 kJ/mol, and for C-Br it is 275 kJ/mol. As you can see, the bond energy values have decreased from C-F to C-Br, meaning that there is more energy input needed to break the C-F bond than the C-Br bond. Thus, the C-F bond is stronger than C-Cl and C-Br bonds. 

Enthalpy Change for a Chemical Reaction

The enthalpy change for a chemical reaction can be calculated using the following mathematical expression:

∆H = ƩD_{bonds broken} - ƩD_{bonds formed}

Where:
∆H – enthalpy change of a chemical reaction
ƩD_{bonds broken} – the sum of the energy required to break all bonds in the reactants
ƩD_{bonds formed} – the sum of the energy released when all bonds are formed in the products
Ʃ – simply means “the sum of”
D – represents the bond energy in kJ/mol

Calculation of an enthalpy change for a reaction provides a rough estimate rather than an exact value since the D values are generally averages for one type of bond in many different molecules.

Let’s consider a specific example:

• H₂(g) + Cl₂(g) → 2HCl (g)
• The reaction above can also be written as:
  H-H (g) + Cl-Cl (g) → 2 H-Cl (g)
• Considering this reaction, we might conclude that 1 molecule of H₂ (or 1 mole of H-H bonds) and 1 molecule of Cl₂ (or 1 mole of Cl-Cl bonds) must be broken to form 2 molecules of HCl (or 2 moles of H-Cl bonds).
• The bond energies found in Table 1 below are the following:
  H-H – 436 kJ/mol
  Cl-Cl – 243 kJ/mol
  H-Cl – 432 kJ/mol
• To calculate the enthalpy change of this reaction, we should use the formula and plug in the bond energy values
  ∆H = ƩD_{bonds broken} - ƩD_{bonds formed} =
        = [D_H-H + D_Cl-Cl] – [D_H-Cl + D_H-Cl] =
        = [436 + 243] – [432 + 432] = -185kJ
• As a result, we get a negative ∆H value, meaning that there is excess energy released in the form of heat. Therefore, the reaction is exothermic. 
• If the calculated ∆H is positive, there is a lack of energy, so the energy is absorbed from the environment. Thus, such a reaction is endothermic. 

Enthalpy Change of a Chemical Reaction Involving Liquids

In the previous cases, all reactants and products were in the gaseous form. 

But what happens if one or more compounds involved in the reaction is a liquid rather than gas?

In such an instance, bond enthalpy cannot be calculated directly from the bond energies of products and reactants. Now, we have to introduce a new term, which is the enthalpy change of vaporization, given by the symbol ∆H_vap or ∆H_v. The term is used to describe the enthalpy change when 1 mole of liquid is converted to gas with a pressure of 1bar (1atm or 100kPa).

It might seem a little bit confusing at first glance, but the calculation of the ∆H or a chemical reaction involving a liquid is quite straightforward. The following steps might be useful for you to understand how to calculate the ∆H value correctly.

1. Identify the compound that is in liquid form (either on the reactants side or the products side; might also be on both sides of the equation);
2. Find the value for ∆H_vap for that specific compound(s);
3. Consider the amount (moles) of the compound consumed or produced in a liquid phase (simply use the stoichiometry);
4. Multiply the ∆H_vap value by the number of moles of the liquid;
5. Now calculate the ∆H using the formula ∆H = ƩD_{bonds broken} - ƩD_{bonds formed,} but do not forget to add the value of ∆H_vap calculated in Step 4 to the corresponding side of the equation.
   For instance, if one of the reactants was a liquid, add the ∆H_vap value to the sum of the enthalpies of reactants (or ƩD_{bonds broken}). In case if one of the products was a liquid, add the ∆H_vap to the sum of the enthalpies of products (or ƩD_{bonds formed}).

Read more about enthalpy and entropy

Table 1 – Bond Energies in kJ/mol

Bond	Bond Energy		Bond	Bond Energy		Bond	Bond Energy
H-H	436		C-S	260		F-Cl	255
H-C	415		C-Cl	330		F-Br	235
H-N	390		C-Br	275		Si-Si	230
H-O	464		C-I	240		Si-P	215
H-F	569		N-N	160		Si-S	225
H-Si	395		N=N	418		Si-Cl	359
H-P	320		N≡N	946		Si-Br	290
H-S	340		N-O	200		Si-I	215
H-Cl	432		N-F	270		P-P	215
H-Br	370		N-P	210		P-S	230
H-I	295		N-Cl	200		P-Cl	330
C-C	345		N-Br	245		P-Br	270
C=C	611		O-O	140		P-I	215
C≡C	837		O=O	498		S-S	215
C-N	290		O-F	160		S-Br	250
C=N	615		O-Si	370		S-Br	215
C≡N	891		O-P	350		Cl-Cl	243
C-O	350		O-Cl	205		Cl-Br	220
C=O	741		O-I	200		Cl-I	210
C≡O	1080		F-F	160		Br-Br	190
C-F	439		F-Si	540		Br-I	180
C-Si	360		F-P	489		I-I	150
C-P	265		F-S	285

IMPORTANT NOTE:

The bond energy values for different bonds vary from source to source. So, the values that are provided in Table 1 above might be slightly different from the values represented in other textbooks. Since these values are roughly estimated, these variations will not have a great impact on the calculated result. Simply use the values that are given in your specific textbook or within the particular problem that you have to solve.

Frequently Asked Questions

What are the bond enthalpies for C-C, C=C and C≡C?

The bond enthalpies for C-C, C=C and C≡C are 345KJ/mol, 611 KJ/mol and 837KJ/mol respectively. The trend of bond enthalpy for carbon-carbon bonds are; bond enthalpy for C-C > C=C > C≡C.

What is bond energy or bond enthalpy?

Bond energy is the energy required to break a bond present in a compound. It is also known as bond enthalpy or bond strength. The bond enthalpy for the sigma bond is greater than that of pi bonds.

What is the trend of bond energy in halogens?

The trend of bond enthalpy for halogen molecules is as follows; “Cl₂ ​> Br_2​ > F₂ ​> I₂. Chlorine shows the highest bond energy among halogens because of its peculiar nature.

What type of energy bond enthalpy is?

Bond enthalpy is the potential energy stored in a chemical bond. This energy is released in the form of heat when this bond is broken down.  For example; energy is obtained by the hydrolysis of ATP in the body due to the breakdown of phosphate bonds.

References:

OpenStax. (2015). “OpenStax, Chemistry.” Retrieved from: http://cnx.org/content/col11760/latest/

If you like what you read, and you're teaching or studying A-Level Biology, check out our other site! We also offer revision and teaching resources for Geography, Computer Science, and History.