Table of Contents
The physical properties of gases are dependent upon 4 variables which are the following:
- Pressure – P
- Volume – V
- Temperature – T (Kelvin)
- Number of moles – n
Several laws describe the changes in the state of gas by defining variable or constant quantities:
- Boyle’s Law – variable pressure and volume; constant temperature and number of moles;
- P1 x V1 = P2 x V2
- Charles’s Law – variable temperature and volume; constant pressure and number of moles;
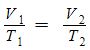
- Gay-Lussac’s Law – variable temperature and pressure; constant volume and number of moles;
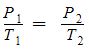
- Avogadro’s Law – variable number of moles and volume; constant pressure and temperature.
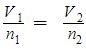
The Ideal Gas Law
An ideal gas is a theoretically characterized gaseous substance that consists of lots of randomly moving particles with interactions of perfectly elastic collisions. The concept is essential since it obeys the ideal gas law, which will be discussed shortly.
Obviously, there is no such concept as an “ideal gas,” but at room temperature and atmospheric pressure, all gases follow the relation of the ideal gas law quite well. For that reason, the ideal gas law has universal applicability and is essential for solving the problems regarding moles or masses of gaseous substances.
Therefore, several assumptions must be considered in the case of ideal gases:
- Ideal gases are composed of constantly and randomly moving particles;
- Molecules which ideal gases are composed of act as rigid spheres;
- All collisions (between the molecules, and between the molecules and the wall of the container) are perfectly elastic, and no kinetic energy is lost during the collision process;
- Pressure arises due to the collisions;
- Intermolecular forces between the gas molecules are completely negligible;
- The volume occupied by the molecules is entirely negligible.
If we combine all 4 variables, pressure (P), volume (V), temperature (T), and the number of moles (n), we get the following mathematical expression:
PV/nT = constant
This constant is defined by the universal gas constant, which is denoted by R.
So, the equation above can be rearranged into its most common form:
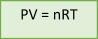
The Ideal Gas Law
R – universal gas constant; was experimentally determined using the concept that any 1mol of gas occupies 22.4L at the pressure of 1atm and temperature of 273K.
Scientists have adopted specific conditions since the volumes of gases are dependent upon the temperature and pressure, and the only way to relate volumes of different gases is to measure them at the same conditions.
These standard conditions, also referred to as standard temperature and pressure (STP) of a gas was determined to be the following:
P = 1.00atm
T = 273K
R = 0.0821 L∙atm/K∙mol = 0.0821 L∙atm∙K-1∙mol-1
Let’s consider each of the variables of the ideal gas equation.
Pressure – P
The pressure is given in atmosphere, or atm. It can also be measured in various units, including pascals, bars, torr, etc.
Be aware that you must always convert the pressure to atm to properly plug the values in the ideal gas equation.
1atm = 1bar = 760torr = 101,325 Pa = 100kPa
Volume – V
Volume is given liters, or L, so make sure that you convert the units to liters before you use the ideal gas equation.
1L = 1,000mL = 0.001m3 = 1,000cm3 = 1dm3
To calculate the volume of a gas using the ideal gas equation, you can use the following formula:
V = nRT/P
Number of Moles – n
The number of moles is, of course, used in moles. To calculate the number of moles, you simply use the concept that 1mol of any gas occupies 22.4L of volume. So, you just divide the given volume of a particular gas by 22.4L to get the amount of that gas in moles.
To calculate the number of moles of an ideal gas using the ideal gas equation, you can use the following formula:
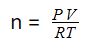
Read more about the Molar Volume of Gases
The Gas Constant – R
As we already discussed above, the value of R is given in units “L∙atm∙K-1∙mol-1.”
R = 0.0821 L∙atm∙K-1∙mol-1
Temperature – T
Temperature is given in Kelvin; therefore, do not forget to convert Celsius or Fahrenheit temperature to Kelvin.
The following conversions might be useful for you:
Kelvin Temperature = Celsius Temperature + 273
Kelvin Temperature = (Fahrenheit Temperature + 460) x 5/9
The Ideal Gas Law and Molar Mass
Using the ideal gas law, you can calculate the molar mass of a particular gaseous compound.
As we know, the number of moles (n) is equal to the mass of a compound (m) divided by its molar mass (M):
n = m/M
As we already discussed above, the number of moles can be calculated from the ideal gas law using the following equation:
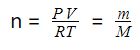
If we solve for M, we get the following equation:
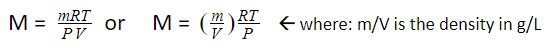
Let’s consider several problems to better understand the concept of the ideal gas law.
Sample Problem:




Summary
It might seem a little bit confusing to choose the proper equation for the problem that you are asked to solve. In reality, it is quite easy to use the needed equation if you try to understand the concept of each one.
The most important thing while solving the problem is to identify the values that you are given. For instance, does the problem provide information about pressure and temperature or volume and number of moles?
As long as you get the idea of what the particular problem is asking for, you can quickly decide which equation would be suitable for that specific scenario.
If there are only two values given, you are most probably asked to calculate something using the 4 equations that we have discussed in the beginning of the article (Boyle’s law, Charles’s law, Gay-Lussac’s law, or Avogadro;s law).
Be aware that if the problem provides details about 2 terms (e.g., temperature and pressure) you can only calculate either temperature or pressure using the 4 laws mentioned above.
If the problem asks you to calculate some other value that is not given in the problem, you might need to use the ideal gas law since the ideal gas equation combines all terms in one equation and makes it possible to calculate, for instance, the number of moles when you are just given temperature and pressure.
All the equations discussed throughout the article are summarized in the table below:
| Boyle’s Law | P1 x V1 = P2 x V2 | Variable pressure and volume | Constant number of moles and temperature |
| Charles’s Law | V1/T1= V2 /T2 | Variable volume and temperature | Constant number of moles and pressure |
| Gay-Lussac’s Law | P1/T1= P2/T2 | Variable pressure and temperature | Constant number of moles and volume |
| Avogadro’s Law | V1/n1= V2/n2 | Variable volume and number of moles | Constant pressure and temperature |
| The Ideal Gas Law | PV = nRT | Variable pressure, volume, number of moles and temperature |
NOTE:
The quantities that are used in a particular equation are called variable quantitis, and the ones that are not mentioned in the equation are called constant quantities.
For instance, in the ideal gas law, all the quantities (pressure, volume, number of moles, and temperature) are variable.
On the other hand in case of the 4 laws mentioned above, 2 quantities are variable and 2 quantities are constant.
Frequently Asked Questions
What is an ideal gas?
An ideal gas obeys all the gas laws completely. The characteristics of an ideal gas are; 1) its molecules should have negligible volume. 2) molecules should have the least or no interactive forces among them. 3) all the collisions among its molecules should be perfectly elastic.
What is Boyle’s law?
Boyle’s law states that; “at constant temperature and no. of moles of gas, the volume of the gas is inversely proportional to the pressure applied on it”. In other words, the product of pressure and volume of gas should remain constant at constant temperature and no. of moles.
What are the standard conditions to apply the ideal gas equation?
The standard conditions of temperature and pressure to apply the ideal gas equation are as follows; 1) Temperature is equal to 273K, 2) pressure is equal to 1.0 atm.
What is R in the ideal gas equation and what is its value at STP?
R is the ideal gas constant which is obtained by the formula PV=nRT or R=PV/nT. Its value at STP is equal to 8.314 J per mole per kelvin when expressed in SI units.
References:
OpenStax. (2015). “OpenStax, Chemistry.” Retrieved from: http://cnx.org/content/col11760/latest/
If you like what you read, and you're teaching or studying A-Level Biology, check out our other site! We also offer revision and teaching resources for Geography, Computer Science, and History.





