Stoichiometry and Balancing Reactions | A-Level Chemistry Revision Notes

Q: What is stoichiometry?

The word stoichiometry has been derived from the Greek words, “stoikhein” which means elements and “meteron” which means “measurement”. So, stoichiometry simply means the quantitative study of the numerical relationship between reactants and products of a reaction.

Q: What are some conventions in stoichiometry?

1) Every element present on one side of a chemical equation must be present on the other side either individually or in a bound state. 2) The number of atoms of an element present on one side of the chemical equation must be equal to the no. of atoms of that element on the other side.

Q: What are the factors to be considered while balancing chemical reactions?

The factors to be considered while balancing a chemical reaction are; molarity, hydrated salts (water of crystallization has significant importance while balancing chemical equations), the charge on the different elements and empirical and molecular formulae of the compound.

Q: Which laws provide the basis for stoichiometry?

The Law of conservation of mass and the law of definite proportions are the ones which provide the basis for stoichiometry and stoichiometric calculations.

Table of Contents

Introduction to Stoichiometry and Balancing Reactions

All chemical reactions depend on the reactant(s) and the conditions under which the reaction occurs. The law of conservation of mass, constant composition, multiple proportions, and reciprocal proportions influence the product(s), ensuring the best path for a reaction under a given set of conditions. Understanding the best possible route for a chemical reaction is included the understanding of the efficiency of the reaction, which gives rise to the question of how much of a reactant is required so that the desired product is yielded at maximum. While exploring the answers to these questions, some common observations are

A particular product or multiple products in a fixed ratio get formed when the reactants get mixed in a definite ratio under identical conditions.
Even if the reactants get mixed in a ratio not represented by the products, the reaction takes place but with unused reactants being leftover.
Same reactants can produce different products if reacted in different ratios.
The ratios of reactants used up in a reaction can depend upon the conditions, such as the presence of a reactive gas like oxygen or unreactive gases like nitrogen and argon.
Acidic or basic conditions alter the reaction speed, the ratio of reactants required, and the product(s).

From these observations, one can identify two basic criteria required for the reproducibility of a chemical reaction:

Identical conditions.
The identical ratio of reactants.

The criterion that deals with the ratio of reactants to determine reproducible quantitative data for a reaction is known as stoichiometry. To achieve this end, one needs to balance the chemical reactions. Balancing implies finding the exact minimum whole number of each atom, either individually or as a part of a molecule or ion, that can participate in a chemical reaction. This, in turn, can be extended to large bulks of chemicals since a mole of any substance contains 6.022 × 10²³ units of that substance.

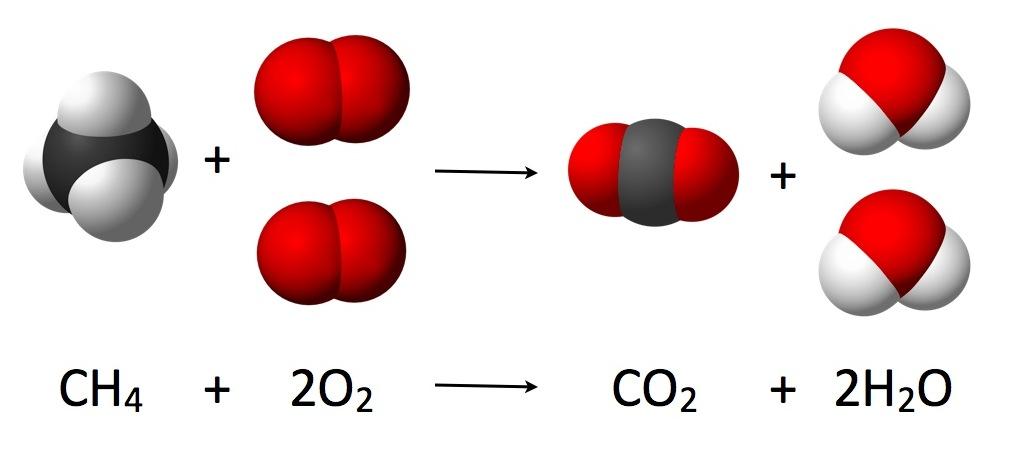
Conventions

A chemical reaction is typically represented by writing the chemical symbols – the symbols for reactants on the left and the symbols for the products on the right, separated by a single or double arrow which indicates the direction and reversibility or irreversibility of the reaction.

The number of atoms on the left side of the equation must be equal to the number of atoms on the right side for a particular element, whether present individually or as a part of one or multiple molecules or ions.

Steps for balancing chemical reactions

1. The species with the highest number of elements should be assigned a coefficient of one (1).

2. Any species with a single element should be balanced at the very last.

3. Fractional coefficients can be converted to whole numbers if required.

4. A final check should be made to see if the number of atoms is equal on both sides of the equation.

States of matter in balancing chemical reactions

Reactions involving species in different states are denoted by the symbols gaseous (g), solids (s), liquids (l), and aqueous (aq). Typically the aqueous state denotes an ionic species and therefore represents a reaction taking place in water wherein the water molecules also need to be balanced quite often.

Factors to be considered for balancing chemical reactions

Molarity - One mole of a substance is the amount of that substance with the same number of specific particles (atoms, molecules, and ions) as there are atoms in exactly 12 g of the carbon-12 isotope. Since this number is constant for a particular atom/ion/molecule and electrons, this can be used to find the coefficients to balance a chemical reaction from the weight of products and/or reactants.

Hydrated salts - Hydrated salts contain water of crystallization. Anhydrous salts do not contain water for crystallization. For example, when hydrated copper sulphate (blue crystalline solid) is heated, anhydrous copper sulphate (white powder) is obtained. Therefore, while balancing a chemical reaction involving hydrated salts, it is to be carefully noted whether the water present takes part in the reaction or not. The removal of crystalline water through heat can also be considered a chemical reaction despite no new compound being formed.

CuSO₄.5H₂O(s) → CuSO₄(s) + 5H₂O (g)

Charge on chemical species

Electrons play the most important role in chemical reactions, and it is most evident in ionic reactions where the charge on a species can completely change the outcome of a reaction. The most common examples are the reactions involving Fe2+/Fe3+, Co2+/Co3+, and Pb2+/Pb4+, wherein the charge on the species can determine the course of the reaction.

Empirical and molecular formula

The simplest formula of a compound is its empirical formula. It represents the number of atoms of each element in its simplest ratio. The molecular formula denotes the actual (total) number of atoms of each element in a compound. It is always a multiple of the empirical formula. The molecular formula can be determined by the empirical formula and relative molecular mass can determine the molecular formula. A balanced chemical reaction's must-have components are denoted by their molecular formula.

Read more about the Reactions of Alcohol

Constructing balanced chemical equations

From the quantitative data obtained in the form of weights of products and reactants, it is possible to determine the ratios of these components. For example, heating lithium carbonate produces lithium oxide and carbon dioxide. This can be denoted as

Li2CO3 + Heat = Li2O + CO2

Element	Number of atoms		Balanced?
	Reactant side	Product side
Li	2	2	Yes
C	1	1	Yes
O	3	3	Yes

The above chemical equation is balanced as the number of atoms for each element is the same on both the reactant and product sides. It is also important to insert information about the states of reactants and products. Here, the states of Li2CO3 and Li2O are solid, while that of CO2 is gaseous. Additional information about the conditions is given above the arrow mark. In this case, the temperature is a crucial factor that should be either denoted by a delta symbol or the exact value.

In another example, let us take the case of lead (IV) hydroxide reacting with sulfuric acid. In the simplest form, this can be represented as

Pb(OH)4 + H2SO4 → Pb(SO4)2 + H2O

On counting the number of atoms on both sides, it is found that the reaction is not balanced. The number of reactant atoms for Pb, O, H, and S are respectively 1, 8, 6, and 1 whereas their numbers on the product side are 1, 9, 2, and 2.

To balance the reaction, this criterion of an equal number of atoms of each element must be fulfilled. The second criterion of balancing the charges is relatively straightforward in this case. Hence, the balanced equation will be:

Pb(OH)4+2H2SO4→Pb(SO4)2+4H2O

Here, the number of Pb, O, H, and S are 1, 12, 8, and 2 on both sides of the equation.

Utility of balancing chemical reactions

1. Information obtainable from balancing a chemical reaction can help in extending further studies and standardising future reactions.

2. Molar gas volume can be obtained from balanced reactions.

3. Using a balanced equation and the number of reactants reacting together, the number of products formed can be found out and vice versa.

4. Solution volume and concentration of the reactants and products can be calculated.

5. Stoichiometry of a reaction can be cross-checked using titration by formulating a plausible reaction route.

6. Identifying limiting and excess reagents. The reactant that is completely used up in a reaction is called a limiting reagent. The reactant that does not get used up completely in a reaction.

Exceptions to stoichiometry

Naturally occurring compounds, mostly minerals of metal oxides, sulfides, and hydrides containing iron, palladium, tungsten, and titanium, often have inconsistent ratios of elements.

Naturally occurring compounds often have inconsistent ratios of elements. Learn more about stoichiometry and balancing reactions

Pyrrhotite is an example of a non-stoichiometric inorganic compound, with the formula Fe_1−xS (x = 0 to 0.2).

Wüstite is written as Fe_1−xO, Palladium hydride as PdH_x (0.02 < x < 0.58), and Tungsten oxides as WnO_3n−2, where n = 20, 24, 25, 40. Apart from these, Prussian blue has also been reported to exist in non-stoichiometric forms.

Frequently Asked Questions

What is stoichiometry?