Atomic Orbital | Types, Energies, Diagram, Examples, Summary

Table of Contents

According to atomic theory and quantum mechanics, an atomic orbital is a mathematical expression that presents the wave-like behaviour of 1 or 2 electrons of an atom. Unlike the fixed-orbit path of planets around the sun, electrons present in an atom don't follow a definite path. Their movement is subjected to quantum mechanics, and it is described using 3-dimensional clouds known as orbitals.

A total of four different orbitals have been discovered to date. They are the s orbital, p orbital, d orbital, and f orbital. The s orbital has the lowest energy as it is closest to the nucleus while the d orbital has the maximum energy as it is farthest from the nucleus.

The Heisenberg Uncertainty Principle

The Heisenberg Uncertainty Principle says that it is not possible to find the current position of an electron and its position an instant later. From this, we can say that it is not possible to calculate the position and momentum of an electron with absolute precision. So, the orbitals actually show the shape of the region where an electron can be found 95% of the time.

The Heisenberg uncertainty principle actually said that for any object in the universe, both the exact position and the exact velocity can not be calculated at the same time even in theory. But we can easily calculate the position and velocity of a car. This is because the uncertainty, in this case, is too small.

Thus, the uncertainty principle is relevant only for the objects with small sizes like an atom.

The uncertainty principle uses the momentum and position factor of a particle, where the momentum is equal to the mass multiplied by the velocity. So, when the uncertainties in momentum and position of a particle are multiplied, it is ≥ h/4pi. This formula is also applicable to an unstable atom.

As there is no certainty of an electron's position, the orbitals are the spaces where the electrons are most likely to be present or are the site of maximum probability of the location of electrons in an atom.

Shapes of orbital

Each orbital has a different type of 3-dimensional shape. The shape of orbitals is determined by the quantum number “l”, and the quantum number “m” determines its orientation. But if the orbital is shown by the equations of complex numbers then the quantum number “m” will show the shape or orbital.

The s-orbitals are of spherical shape as the quantum number l = 0. The density of electrons is seen the most near the centre of the atom, and the density reduces as we move away from the nucleus. This looks like a solid ball.

But for n = 2 or more, there are spherically symmetrical shells which means that there is a radial wave-structure with a sinusoidal radial component.

An antinode can be observed at the centre of the nucleus in s orbitals irrespective of their n numbers. These antinodes are found only in the s orbitals as all the other orbitals p,d,f, etc. have angular momentum and stay away from the nucleus.

The 3p orbitals with the value of n equal to 2 have a unique shape with 2 ellipsoids having a point of tendency at the nucleus like a dumbbell.

The shape of d orbitals is like clover or a double-dumbbell. This shape is because, during rotation, the electron is pushed four times outside.

The shape of f orbitals has a tetrahedral shape.

Here is a picture of the shape of all four types of orbitals. The f orbital has a complex shape. It looks like the d-orbital except that it has four dumbells and the d orbital has 2 dumbbells.

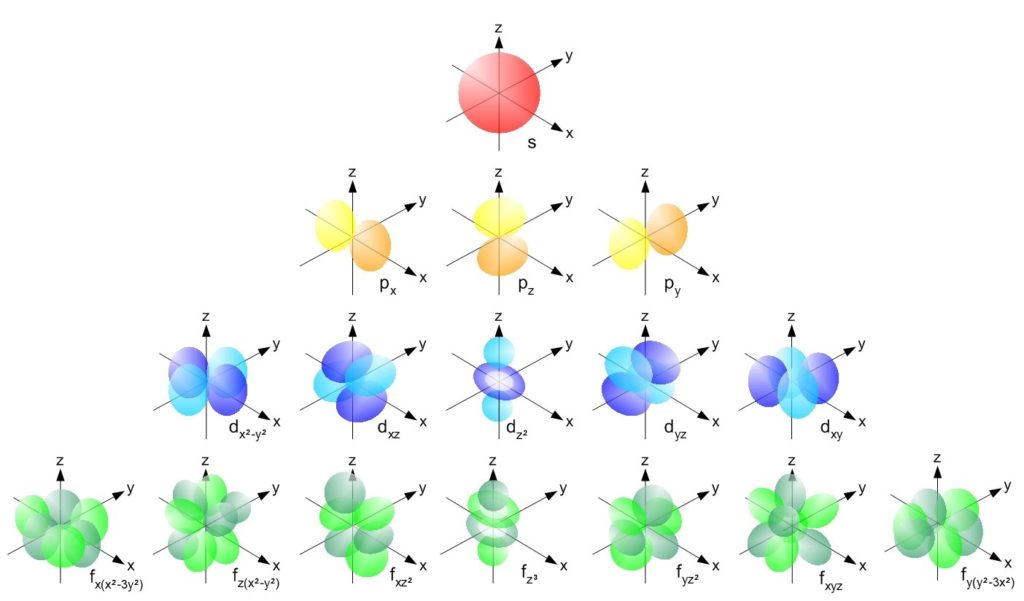
The naming of atomic orbitals

A different set of values of the 3 quantum numbers n (energy), l (angular momentum), and m (magnetic moment) are used to characterize each orbital in an atom. These orbitals can contain a maximum of 2 electrons. s-orbital, p-orbital, d-orbital, f-orbital are the orbitals having the angular momentum quantum number as 0,1, 2, and 3 respectively. These orbital names along with energy quantum number n are used to describe the electron configuration of an atom.

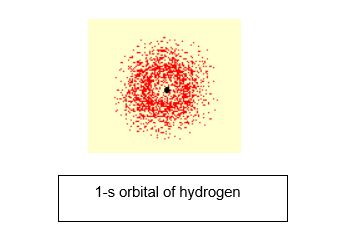
Let’s see an example.

For a hydrogen atom, if we plot its position at an instant and then again plot its position after some time, we will find that it is at a different position this time. If we do it repeatedly, then it will find a spherical shape around the nucleus. 1-s orbital is the orbital occupied by hydrogen, where “1” says that orbital has the energy level closest to the nucleus, and “s” here stands for the spherical shape.

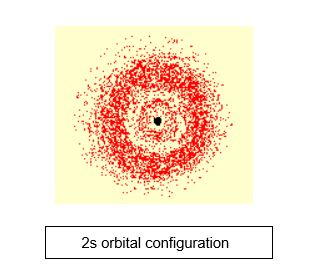
In the 2s orbital, “2” represents that the energy level is further from the nucleus and like 1s, “s” represents the spherical shape of the orbitals.

While the energy level of an electron is indicated by the orbital numbers, i.e. n = 1, 2, 3, the orbital shape of an electron is described by letters s, p, d, f.

s orbital

As said above, orbitals are the region where an electron can be found. s-orbitals means that those regions are spherical-shaped. This spherical region is further divided into shells as 1s, 2s, and 3s orbital. The 1s shell is closest to the nucleus and is the smallest in size. The 2s orbital is bigger than 1s and 3s is even bigger.

Number of electrons in an orbital

Let’s say “l” is the angular quantum of the subshell, then the maximum number of electrons it can hold can be calculated as 2(2l+1)

When l= 2, then the electrons will be 2[(22) +1] = 10 electrons. ‘l’ is 2 for d orbital so, d-orbital can have a maximum of 10 electrons in it.

So, the maximum number of the electrons that can accommodate in carious orbitals are:

1. s orbital: 2 electrons

2. p orbital: 6 electrons

3. d orbital: 10 electrons

4. f orbital: 14 electrons

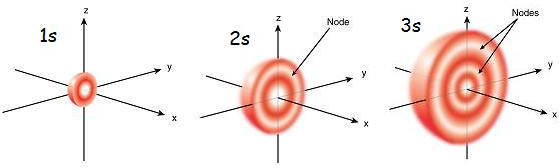
Diagram of 1s, 2s, and 3s orbitals

In 1s orbital, the density of electrons is found to be very low near the nucleus, but as we go further from the nucleus, its density increases to attain the peak value and then decreases. In 2s orbital, the outer sphere of electrons contains one more sphere of electrons. To understand how the 2s look, imagine 2 hollow tennis balls with a tennis ball inside another.

Between these 2 spheres of the electron sphere is a region with no probability of finding electrons, called nodes. The 3s orbital is similar to 2s orbital, but it has 3 spheres of electrons unlike 2 spheres in 2s, and also has 3 nodes.

Properties of electrons

The quantum mechanics and some experimental findings suggest that the electrons are not fully particles; they can be explained by the wave-particle duality.

Wake-like properties

As discussed above that the motion of electrons is not like the motion of planets around the sun, they are present as standing waves, i.e. they appear to be moving in the vertical plane but not in the horizontal plane.

Particle-like properties

The number of electrons present in the orbits is always an integer.
The electron always jumps between orbitals like a particle.
For electrons, each wave state retains the electrical charge of its electron particle.

Bohr’s model

This explains the way electrons can have stable orbits around the nucleus, Bohr proposed the quantized shell model. In Rutherford’s model, the motion of the electrons was not stable because when a particle carrying a charge moves in a curved path, it emits electromagnetic radiation and due to this, the electron will be losing energy and will eventually fall into the nucleus.

Bohr solved the stability problem by suggesting that electrons will move in the orbits of definite size and energy, with the smaller orbits having lower energy. Also, radiation will be released only when an electron jumps between the orbits.

Thus, the smallest orbit will contain the most stable atom as there will not be any orbit.

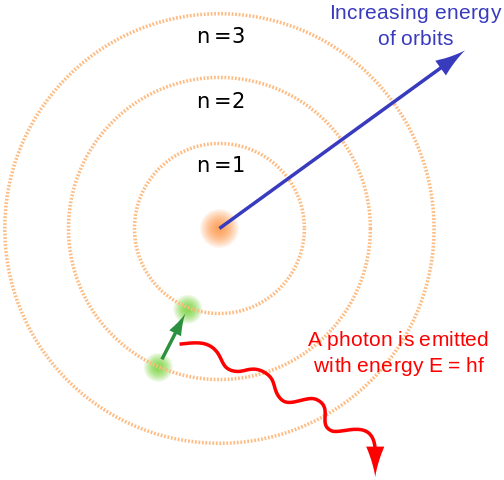
Bohr’s model

Bohr realised that classical mechanics independently is not able to explain the atom’s stability. An atom in a stable state must have a definite size, for any equation describing it to have some fundamental constant or combination of constants with length’s dimension. He realised that Planck's constant contains dimension and can give a measure of length when combined with the electron's charge and mass. This gave a number close to the size of atoms.

Bohr obtained an accurate formula for the energy levels of the hydrogen atom using Planck's constant. He suggested that it is due to quantization only that the orbits of electrons have fixed size and energy, therefore “l”, i.e. angular momentum is quantized for electrons. Using this model Bohr explained that only by absorbing or emitting energy electrons can jump between the orbits. So, when an electron has to jump to an orbit closer to the nucleus, then energy has to be emitted by it and when an electron has to jump from an orbit closer to the nucleus i.e. smaller in size to a larger orbit, then it has to absorb energy.

Understanding the notation of orbitals

The general form in which orbitals are given names: n(type)_x

Here, “n” is the energy level of the principal quantum number n.

“type” shows the shape of the orbital of the angular quantum number l.

“x” shows the total electrons present in the orbital.

So, the notation for 2nd energy level and p orbital is 2p_x

Example: 2s² orbital explains that there are 2 electrons present in the second energy level with a spherical shape.

X-ray notation

This is a type of notation used for orbitals and was given by the International Union of Pure and Applied Chemistry (IUPAC) in 1991. It was developed with the help of X-ray science. This is a traditional method of notation and s less commonly used. In this notation, the orbitals are given the alphabets instead of the quantum numbers. The quantum numbers 1, 2, 3, and 4 are denoted by alphabets K, L, M, and N respectively. The shells are denoted by using a number in superscript on their right.

For example, For 2p orbital, the X-ray or IUPAC notation is L₂, where L is the quantum number and 2 is for p shell.

Hydrogen like orbitals

A system that has only 1 electron is the simplest atomic orbital, like a hydrogen atom. If an atom of other elements is ionised to a single electron, then it will also resemble hydrogen. The atomic orbitals, according to the Schrodinger equation for hydrogen-like elements, are eigenstates of the Hamiltonian operator. These can be measured analytically, which means that they are the product of exponential functions, trigonometric functions and polynomial series.

An atomic orbital can be identified whether it is a hydrogen-like orbital or not by the 3 quantum numbers n, l, and m which are electron energy, total angular momentum quantum number, and magnetic moment respectively.

Aufbau’s principle

The word Aufbau translates to “construct or build-up”. This principle shows the standard way in which electrons fill the atomic orbitals of atoms in the ground state. According to this electrons occupy the atomic orbitals as per the energy levels. The atomic orbitals with lower energy levels are filled before the orbitals with higher energy levels.

The diagram below shows the sequence in which the atomic orbitals are filled.

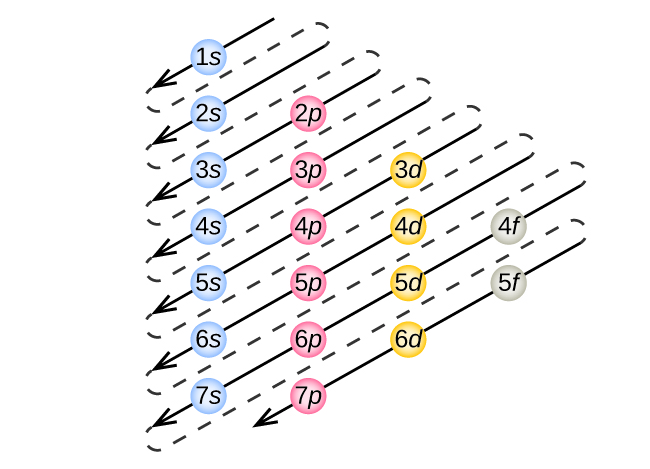
The sequence of orbitals occupied by electrons

So, the order for arrangement of electrons is:

1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, and 7p

After the introduction of this principle, it became very easy to understand and find the location of electrons present in an atom and also their energy levels.

Let’s see an example of this. As carbon has 6 electrons, then according to Aufbau’s principle the first 2 electrons will occupy the 1s orbital, then 2 in 2s and 2 electrons will occu[y the 2p orbital. Thus the electron configuration of carbon becomes 1s² 2s² 2p².

In this process, the two principles, i.e. Pauli’s exclusion principle and Hund’s rule, should also be followed.

Pauli's exclusion principle

Pauli’s exclusion principle says that each orbital can occupy a maximum of 2 electrons and both the electrons have opposite spins. This principle explains the structure of the electron shells. It explains the formation of chemical bonds between two elements.

Hund’s rule

Hund’s rule says that each orbital of the subshell must be filled with one electron first. Once all the orbitals of each subshell have one electron, only then the pairing of the electron should take place in any orbital. This is because electrons have a negative charge and they have the ability to go to the empty shells first to avoid repulsion. Once all the shells have electrons, the electrons start to pair up. Contrary to Pauli's exclusion principle, it also states that the electrons in an orbital have the same type of spin.

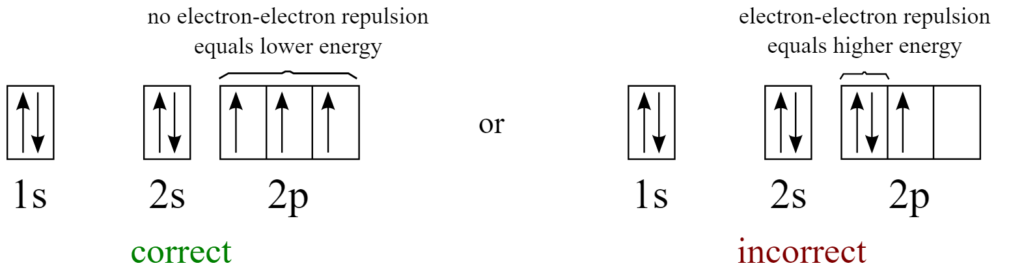
This means that as there are 2 orbitals for n = 2, from the remaining 4 electrons (after filling 1s orbital) must fill in this manner, 1 electron goes in 2s, the next electron goes in 2p then the 5th electron goes to the 2s to form pair and the last electron in 2p.

Similarly, for Fluorine with atomic number 9, the total number of electrons will also be 9. Its electron configuration will be like this:

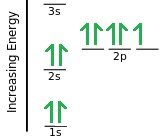
For the 1s orbital 2 electrons have been paired, then for 2s and 2p orbital, out of the remaining 7 electrons, initially 1 electron is occupied in each orbital ( 2s has 1 orbital, and 2p has 3 orbitals), and then pairing of electrons take place. So, the last orbital if 2p does not have its electron paired.

Note: To decide which orbital will be filled first as per energy level, the (n+l) rule can be used. The lower (n+l) value shows that the orbital has lower orbital energy, and it will be filled first.

Electronic configuration

The electronic configuration is the distribution of electrons in the orbitals. All the notations and the principles of the alignment of the electrons in orbitals help to write the electronic configuration of an atom of the element.

Summary:

Orbitals are the regions where electrons are most likely to be found.
Heisenberg’s uncertainty principle explains that we can not determine the exact location and velocity of electrons.
The orbitals s, p, d, f explains the shape of the orbitals too and when combined with the quantum number “n”, they explain the electron configuration.
The maximum capacity of a subshell to hold the electrons is 2(2l+1), where ‘l” is the angular momentum quantum number.
Electrons are not completely particles, and they can be explained only with the wave-particle duality.
Bohr’s model suggested that an electron can jump between the orbitals only by absorbing or releasing the energy.
Aufbau principle explained the sequence in which electrons occupy the orbitals, i.e. the lowest energy orbitals will be filled first.
Hund’s rule and Pauli's’ exclusion principle are used along with the Aufbau principle to decide the distribution of electrons in the orbitals. These help to determine the electronic configuration of an atom.

Frequently Asked Questions

What is meant by atomic orbital?

An atomic orbital is an expression that describes the location and wave-like behaviour of electrons revolving around the nucleus. It helps to estimate the probability of finding an electron at specific locations around the nucleus.

What are the different atomic orbitals?

There are four atomic orbitals: s, p, d, and f.

What is the lowest energy orbital?

1 s is closest to the nucleus of an atom and is the lowest energy orbital.

How many electrons can be accommodated in different orbitals?

Orbitals hold a different number of electrons; s orbital accommodates 2 electrons, p orbital accommodates 6, d orbital accommodates ten, and f orbital accommodates 14 electrons.

References:

If you like what you read and you're teaching or studying A-Level Biology, check out our other site! We also offer revision and teaching resources for Geography, Computer Science, and History.